1. Definiciones
La estadística descriptiva tiene como objetivo recoger,
analizar, y organizar un conjunto de datos en tablas y gráficos para calcular
unos valores que representen a dicho conjunto.
La estadística estudia las propiedades o cualidades de un
colectivo al que llamamos población.
Si la población es muy grande tomamos una parte representativa de ésta a la que
llamaremos muestra.
Se define el carácter estadístico como la propiedad que permite clasificar a los
individuos de una población. Puede ser de dos tipos:
- Carácter cualitativo: no se
pueden medir, como el color de ojos, profesión…
- Carácter cuantitativo: si se
pueden medir, como número de hijos, altura, peso…
El conjunto de valores que puede tomar este carácter se
llama variable estadística.
Las variables estadísticas son de dos tipos:
- Variable estadística discreta: cuando
toman valores puntuales, por ejemplo, el número de alumnos.
- Variable estadística continua: cuando
puede tomar cualquier valor dentro de un intervalo, por ejemplo, los km
recorridos por un coche.
2.
Tablas de frecuencias
Consideramos
una población de n individuos, de los que estudiaremos un carácter estadístico
A que puede tomar k valores posibles A1, A2…Ak
Frecuencia absoluta: es el número de individuos que presentan cada valor de la variable. Se
representa como fi
Frecuencia relativa: es el cociente entre la frecuencia absoluta y el número total de
individuos. Se representa como hi y se calcula hi = fi
/ n
Frecuencia
absoluta acumulada: se obtiene sumando la frecuencia absoluta de cada fila con las
anteriores, se representa como Fi
Frecuencia relativa acumulada: se obtiene sumando la frecuencia relativa de cada fila con las anteriores, se
representa como Hi
Si la variable estadística es continua hay que agrupar los valores en intervalos, al punto medio de cada uno se le llama marca de clase y se representa como xi
Si la variable estadística es continua hay que agrupar los valores en intervalos, al punto medio de cada uno se le llama marca de clase y se representa como xi
EJERCICIOS
1- Supongamos que tiramos un dado 10 veces y se obtienen los siguientes resultados: 1, 2, 4, 5, 6, 1, 2, 3, 5 y 3. Calcula la frecuencia absoluta, relativa y las frecuencias acumuladas.
1- Supongamos que tiramos un dado 10 veces y se obtienen los siguientes resultados: 1, 2, 4, 5, 6, 1, 2, 3, 5 y 3. Calcula la frecuencia absoluta, relativa y las frecuencias acumuladas.
2- Se anota la altura de
10 personas: 166, 158, 175, 179, 169, 172, 162, 168, 171 y 177. Calcula la
frecuencia absoluta, relativa y las frecuencias acumuladas.
Solución
EJERCICIO
Completa los datos que faltan en la siguiente tabla, donde fi , Fi y hi son la frecuencia absoluta, acumulada y relativa.
Solución
Solución
EJERCICIO
Completa los datos que faltan en la siguiente tabla, donde fi , Fi y hi son la frecuencia absoluta, acumulada y relativa.
Solución
3.
Representaciones
gráficas
Los gráficos estadísticos nos permiten obtener una idea visual y global de la distribución de los datos. Los más usados son los siguientes:
Los gráficos estadísticos nos permiten obtener una idea visual y global de la distribución de los datos. Los más usados son los siguientes:
a) Diagrama de barras: Tienen una base
constante y la altura es proporcional a la frecuencia absoluta correspondiente,
las barras deben estar separadas. Se utilizan para variables cualitativas y
cuantitativas discretas.
b) Diagrama de sectores:
Dividimos un círculo en sectores de área proporcional a cada frecuencia
absoluta. Para ello, mediante regla de 3, calculamos el ángulo correspondiente
a cada sector. Se utilizan para variables cualitativas y cuantitativas
discretas.
360 o --- n
α ---
fi
c) Histograma:
Se construyen rectángulos que tienen como base
la amplitud del intervalo y su altura es la frecuencia absoluta del intervalo
correspondiente. Se utilizan para variables continuas y
discretas.
d)
Polígono de frecuencias: Se construye a partir
del diagrama de barras o del histograma, uniendo los puntos medios de la parte
superior de cada rectángulo.
e) Pictogramas: Son dibujos referidos al carácter estadístico estudiado, donde el
tamaño de los mismos es proporcional a las frecuencias absolutas
correspondientes.
EJERCICIOS
1- Se pregunta a 12 alumnos el número de hermanos que tienen y contestan 0, 1, 2, 3, 2, 0, 2, 2, 0, 2, 3 y 2. Construye la tabla y representa los datos en un diagrama de barras y de sectores.
2- Se obtienen las siguientes notas en una clase de 20 alumnos: 6, 7, 9, 2’5, 4, 8’5, 7, 6’5, 9, 8, 3’5, 4’5, 5, 6, 7, 9’5, 8, 6’5, 3 y 7’7. Calcula su tabla de frecuencias y representa el histograma y polígono de frecuencias.
1- Se pregunta a 12 alumnos el número de hermanos que tienen y contestan 0, 1, 2, 3, 2, 0, 2, 2, 0, 2, 3 y 2. Construye la tabla y representa los datos en un diagrama de barras y de sectores.
2- Se obtienen las siguientes notas en una clase de 20 alumnos: 6, 7, 9, 2’5, 4, 8’5, 7, 6’5, 9, 8, 3’5, 4’5, 5, 6, 7, 9’5, 8, 6’5, 3 y 7’7. Calcula su tabla de frecuencias y representa el histograma y polígono de frecuencias.
Solución
EJERCICIO
El número medio de días que practican deporte un grupo de personas es:
Solución
EJERCICIO
El número medio de días que practican deporte un grupo de personas es:
4 2 3 1 3 7 1 0 3 2
6 2 3 3 4 6 3 4 3 6
Haz una tabla de frecuencias y represéntala gráficamente. Solución
4.
Medidas características
Para estudiar una distribución de
frecuencias, conviene dar algunas medidas objetivas que describan el
comportamiento de los datos. Esas medidas se agrupan en las siguientes categorías:
a)
Medidas de centralización:
Son aquellos valores que representan a
la distribución de frecuencias en su conjunto.
- Media aritmética:
es la suma de todos los
valores de la variable, dividido por el número de ellos.
- Mediana: es el valor de la variable que
divide en dos partes iguales los individuos de la población, una vez ordenados
estos de menor a mayor.
Calculamos N/2,
la mediana será el valor xi de la variable cuya frecuencia
absoluta acumulada, Fi, sobrepase N/2.
Si
la variable es continua se calcula de la siguiente forma:
- Moda: es el valor de la variable que
más se repite, es decir, el que presenta mayor frecuencia absoluta, fi.
Si
la variable es continua se calcula de la siguiente forma:
b)
Medidas de posición:
Estas medidas dan los valores de algunas posiciones de interés en el
conjunto de los datos.
- Cuartiles:
Si en lugar de partir la totalidad de los
individuos en dos mitades (mediana), lo hacemos en cuatro partes iguales,
obtenemos los cuartiles.
Q1: calculamos N/4
y nos quedamos con el primer valor de Fi que sobrepase dicho valor, Q1
será el valor que tome xi en esa fila.
Q2: este valor
coincide con la mediana.
Q3: calculamos 3N/4
y nos quedamos con el primer valor de Fi que sobrepase dicho valor,
Q3 será el valor que tome xi en esa fila.
Si la variable es continua se calcula de la siguiente forma:
- Deciles: Dividen los datos en diez partes iguales.
Si la variable es continua se calcula de la siguiente forma:
- Deciles: Dividen los datos en diez partes iguales.
Hay 10 deciles y se calculan como
los cuartiles pero para cada decil Dk calculamos kN/10
Si la variable es continua se calcula de la siguiente forma:
Si la variable es continua se calcula de la siguiente forma:
- Percentiles:
Dividen los datos en cien partes iguales.
Hay 100 percentiles y se calculan
como los cuartiles pero para cada percentil Pk calculamos kN/100
Si la variable es continua se calcula de la siguiente forma:
Si la variable es continua se calcula de la siguiente forma:
EJERCICIOS
1- Dada la siguiente distribución del número
de hijos de 100 familias, calcular la media
, Me, Mo, Q1, Q2, Q3, D10
y P70.
2- De una ciudad, se ha tomado una muestra sobre la renta percibida. La información recogida es la siguiente:
Calcular la
media, Me, Mo, Q1, D5
y P90.
Solución
EJERCICIO
Un test de 80 preguntas ha sido realizado por 600 personas. El número de respuestas correctas se refleja en esta tabla:
Calcula la media, Me, Mo, Q1, Q3, P20 y P85
Solución
c) Medidas de dispersión:
Estas
medidas indican si los datos están más o menos agrupados en torno a un valor
central. Los datos estarán más agrupados, cuanto más cerca de cero esté el valor
de la medida.Solución
EJERCICIO
Un test de 80 preguntas ha sido realizado por 600 personas. El número de respuestas correctas se refleja en esta tabla:
Calcula la media, Me, Mo, Q1, Q3, P20 y P85
Solución
c) Medidas de dispersión:
- Rango o recorrido: es la
diferencia entre el mayor y el menor valor de la variable.
- Varianza: es la media de los cuadrados de las diferencias respecto a la media.
- Desviación típica: es la raíz cuadrada
positiva de la varianza.
- Coeficiente de
variación de Pearson: permite
comparar varias distribuciones y ver cuál está más dispersa respecto de la media se define como:
EJERCICIO
Dada la siguiente distribución del número de hijos de 100 familias:
Calcular varianza, desviación típica y
coeficiente de variación.
Solución
EJERCICIO
Un test de 80 preguntas ha sido realizado por 600 personas. El número de respuestas correctas se refleja en esta tabla:
Calcula la varianza, desviación típica y coeficiente de variación.
Solución
Podéis seguirme en facebook, twitter y youtube para estar
informados de todas las novedades, ejercicios...
Solución
EJERCICIO
Un test de 80 preguntas ha sido realizado por 600 personas. El número de respuestas correctas se refleja en esta tabla:
Calcula la varianza, desviación típica y coeficiente de variación.
Solución






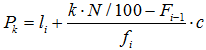






Gracias😊 ahora lo entiendo más mejor 👌
ResponderEliminar